Dråbemodellen i forhold til emnet atombomben
Hej Malte
Jeg går på STX, og har fysik på A niveau. Jeg har valgt at skrive SRP i fysik/historie omkring emnet atombomben.
Da jeg tidligere i AT forløb har arbejdet med Manhattan Projektet, er der visse begrænsninger for hvad jeg kan komme ind på, altså rent fysik fagligt. Min lærer har foreslået mig at arbejde med dråbemodellen, som vi kun har haft meget lidt undervisning om.
Da jeg har haft svært ved at finde litteratur om emnet, skriver jeg nu til dig i håb om at
du kan hjælpe mig. Hvadenten det så er med relevant forslag til litteratur, eller om du har en god idé til hvordan man kan anskue dråbemodellen i forhold til emnet atombomben.
Mange venlige hilser
J
Tak for mailen om dråbemodellen for atomkerner. Jeg har heller ikke kunnet finde nogen fin beskrivelse på dansk om den, men her kommer et par hints:
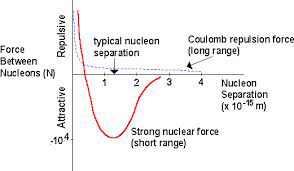
Kernekræfter
Hvis man Googler "liquid drop model nuclear fission" kommer der blandt andet meget
fine illustrative billeder frem, hvor man forestiller sig en tung atomkerne starte som kugleformet, for derefter at blive ramt af en neutron, hvorefter der kan ske tre ting:
- Den kan udsende neutronen igen.
- Den kan udsende en gamma-stråle.
- Den kan vibrere, strække sig, og når den er nået en vis udstrækning, vil
frastødningen mellem protonerne i kernen få den til at strække sig endnu mere, og den vil til sidst gå i to stykker.
- Man kan også Google "liquid drop model nucleus", og kan derefter se på nogle
andre billeder. Blandt andet er der tæt på toppen en illustration af hvad væskedråbe modellen virkelig går ud på. Nemlig at stille en formel op for bindingsenergien af protoner og neutroner til hinanden i kernen: Denne formel har fem led, som nogenlunde kan forklares sådan:

Leidenfrosts forsøg, en vanddråbe svævende på damphinde i hult metalkar, svingninger
1) Volumenenergi ("volume" på figuren) Protoner og neutroner tiltrækker hinanden på
ret kort afstand, så hver proton eller neutron i kernen føler tiltrækningen fra naboerne.
Det giver et positivt bidrag til bindingsenergien - proportionalt med kernens volumen.
2) Overfladeenergi ("surface") Men så har man talt for meget binding med, idet protoner
og neutroner på overfladen mangler tiltrækning fra naboer. Det giver et negativt
bidrag til bindingsenergien - proportionalt med kernens overflade.

Los Almos, Manhattan projektet
3) Coulomb energi ("Coulomb") Coulomb står for elektrostatisk tiltrækning eller frastødning, i det aktuelle tilfælde frastødning. Neutronerne vekselvirker kun med andre neutroner og med protoner over en kort rækkevidde. Men protonerne er jo elektrisk ladede, og de frastøder hinanden tværs hen over hele kernen. Det giver et negativt bidrag til bindingsenergien, ("Coulomb") stort set proportionalt med kvadratet på antal protoner divideret med radius af kernen.
4) Symmetri energi ("Asymmetry") Hvis man indenfor et volumen skal anbringe mange ens partikler (i det aktuelle tilfælde protoner eller neutroner), skal man anbringe dem i højere energitilstande på grund af Pauli princippet. Det giver et negativt bidrag til binndingsenergien ("Asymmetry energy"), som er proportionalt med kvadratet af forskellen på antal neutroner og protoner divideret med volumen af kernen
5) Det sidste led - par enegien - er lille, og det ser vi bort fra her, skønt det faktisk er det der
bestemmer forskellen mellem 238 U og 235 U med hensyn til fission. (Lidt længere nede på siden er formlen givet: "The Weizsaeker Formula", men den er lidt svær at forstå)

Oak Ridge, Uranseparation af Uran 235
- Ud fra væskedråbemodellen kan mange egenskaber af atomkerner forstås:
Det periodiske system afsluttes et sted omkring Bly eller Uran: For tungere og tungere kerner vil Coulombenergien få en større og større betydning. Kernerne bliver da ustabile i den forstand at bindings-energien per proton eller neutron aftager, og der bliver da nok energi til at udsende en alfa partikel (Helium kerne) med pæn stor energi. Endnu tungere kerner vil spontant gå i stykker ved fission, uden at behøve at absorbere en neutron først.
- Hvis en kerne strækkes, ændres volumen- og symmetrienergien ikke. Overfladeenergien er en slags overfladespænding, som vil forsøge at holde kernen sammen, mens Coulombfrastødningengen vil søge at rive den i stykker. For lette kerner vinder overfladespændingen, for meget tunge kerner vil Coulomb-frastødningen mellem protonerne vinde, og de kan derfor ikke være stabile.
- De mest stabile kerner er Jern-Nikkel kerner. Her er der en pæn volumen energi, (der er det eneste positive bidrag til bindingsenergien). Overfladen er ikke så stor i forhold til voluminet som for de lettere, og derfor knapt så stabile kerner. Og sidst, men ikke mindst, den elektro- statiske frastødning mellem protonerne (Coulomb energien) er ikke blevet rigtig stor, som den bliver det for de tungere kerner.
- De lette kerner har nogenlunde lige antal protoner og neutroner - på grund af symmetrienergien. Således har den mest stabile ilt - isotop 8 protoner og 8 neutroner. For tunge kerner kan det godt betale sig at have flere neutroner end protoner - og det bliver en slags konkurrence mellem symmetri-energien og Coulomb-frastødningen, der afgør hvor mange. Den mest stabile bly-isotop har 82 protoner og 126 neutroner.
Med venlig hilsen
Thomas Døssing
