Ioniserende stråling og Bohr modellen
Hej Spørg om Fysik
Bohrs atommodel kan bruges til at forklare det synlige (og lys i det infrarøde og ultraviolette spektrum) lys som fotoner, der udsendes som følge af elektroners spring imellem skallerne (forskellige energitilstande). Jo større spring i energitilstande, jo højere energi (og jo kortere bølgelængde) i de fotoner der udsendes. Og hvert grundstof kan udsende fotoner med helt specifikke bølgelængder.
Ioniserende stråling kan med denne model forstås som stråling, der har så meget energi, at det slår elektroner ud af atomets system for ikke at vende tilbage til sin grundtilstand.
Men hvor mange energitilstande er mulige - f.eks. i et hydrogenatom? Er ioniseringsenergien en grænseværdi således at alle fotoner med en bølgelængde kortere end den "første ioniseringsenergi" ioniserende?
Jeg håber mine spørgsmål giver mening.
Med venlig hilsen
M B
Ioniserende stråling defineres ved, at der sker ionisering af det stof strålingen går igennem. Det er normalt i MeV området. Der indgår altså 2 ting i dette nemlig ioniseringsenergien af det pågældende stof og strålingens energi (bølgelængde, hvis det er elektromagnetiske bølger).
Man opfatter ionisering, som løsrivelse af en elektron, så den føres ”uendeligt” langt væk, dvs. udenfor det område, hvor atomets elektriske felt gør sig gældende. Man anser de bundne elektroners energi som værende negativ, og den tilførte energi slår dem så ud fra atomet til et punkt uendeligt langt væk (i atomar målestok).
| Grundstof | 1. elektron | 2. elektron | 3. elektron | 4. elektron | 5. elektron | 6. elektron | 7. elektron |
|---|---|---|---|---|---|---|---|
| H (Brint) | 13,6 | ||||||
| He (Helium) | 24,6 | 54,4 | |||||
| Be (Beryllium | 9,3 | 18,2 | 153,9 | 217,7 | |||
| Na (Natrium) | 5,1 | 47,3 | 71,6 | ||||
| Mg (Magnesium) | 7,6 | 15 | 80,1 | ||||
| Al (Aluminium) | 6 | 18,8 | 28,4 | 120 | |||
| S (Svovl) | 10,4 | 23,3 | 34,9 | 47,2 | 72,6 | 88,1 | 281 |
| Ar Argon) | 15,8 | 27,6 | 40,7 | 59,6 | 74,8 | 91,3 | 124,4 |
Grundstofferne har forskellige ioniseringsenergier. I skemaet er anført et udvalg. Som det fremgår, kan man i princippet fjerne alle elektroner fra et grundstof, men det kræver mere og mere energi at gøre det, efterhånden som et antal elektroner er fjernet. Der kommer et stort spring når man når ædelgas konfiguration (f.eks. Beryllium 3. elektron, Aluminium 4. elektron, Svovl 7. elektron).

Tågekammerbillede som viser ioniserende stråling i luft
I et givet stof vil alle energier, der kan tilføres fra stråling, og som er større end ioniseringsenergien, altså kunne give anledning til ionisering, dvs. alle fotoner mm. med kortere bølgelængde end svarende til ioniseringsenergien, kan fremkalde ionisering. Det gælder også ved passage af ”ioniserende partikelstråling”, som alfastråling, betastråling, protonstråling og andre ladede ioner, som altså kan ionisere stoffet ved passage. Man bruger ofte betegnelsen ioniserende stråling, i forhold til ionisation af atmosfærisk luft, men principielt kan det være et hvilket som helst stof.
Man inddeler følgende typer af elektromagnetisk stråling, som ikke ioniserende stråling.
UV området fra 100 – 400 nm eller 3000 – 750 THz. Dette svarer til 12,4 til 3,10 eV.

Balmerserien i det synlige spektrum
Energier større end 12,4 eV (bølgelængder kortere end 100 nm) er altså ioniserende stråling. Som det fremgår af oversigtsskemaet, vil fotoner fra mange af stofferne, som ioniseres, være klassificeret som ikke ioniserende i normal luft.
Solens elektromagnetiske spektrum på jorden indeholder ikke ioniserende stråling, men solen udsender store mængder partikler, som er ioniserende. De fleste opfanges i jordens magnetfelt, og indgår i van Allan bælterne, frembringer nordlys mm., men nogen kommer igennem til jorden. Også fra andre kilder i rummet end solen rammes vi ioniserende stråling, det gælder specielt under høje flyvninger.
Bohrs formel, Balmer formelen, for brints energitilstande kan skrives:
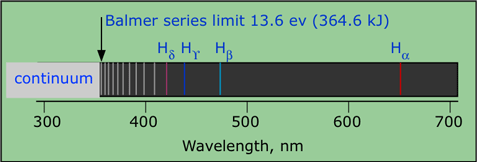
Balmerserien hvor seriegrænsen i UV er med
1/λ = R*(1/m2 – 1/n2) hvor λ er bølgelængden af strålingen, R er den såkaldte Rydbergkonstant, n er nummeret på det laveste energiniveau springet sker fra/til, m det højere niveau. Se også: Hydrogens linjespektrum >>
Hvis n = 1 kaldes de fremkomne bølgelængder Leymanserien, de ligger i UV området, Balmerserien har n=2 og her ligger en del linjer i det synlige område men seriegrænsen, den mest energirige del, ligger i det nære UV området. Der er en række linjeserier for n= 3,4,5 osv. Som det fremgår af formlen, kommer linjerne til at ligge tættere og tættere, når man nærmer sig ionisationsgrænsen, der er matematisk set uendeligt mange i hver serie.
Med venlig hilsen
Malte Olsen
