Riffelskydning

Hej Spørg om Fysik
Håber i kan hjælpe med et væddemål. 

Hvis man i den ene hånd holder en riffel vandret på jordens overflade, og i den anden hånd holder en kugle magen til den der er i riflen i samme højde som riffelmundingen.

Hvis man affyrer riflen og slipper kuglen samtidig, hvilken af kuglerne rammer jorden først?

Modvirker riffelkuglens fart jordens tiltrækningskraft? - eller trækker jorden lige meget i dem begge, således at de rammer samtidig? Håber i forstod spørgsmålet.

På forhånd tak -  en nysgerrig Grønlænder
S B 

Lille billede fra forrige side: På billedet ses et afskudt projektil  og chok fronten fra eksplosionen.

Tyngdekraftens træk i to ens legemer i samme afstand fra jordcentret dvs. her samme højde over jordoverfladen er præcis ens. Et legemes fart betyder ikke noget for hvor kraftigt tyngden påvirker legemet.

Riffelkuglen (fra en gammeldags forlader) og den kugle man slipper med fingrene falder derfor principielt lige hurtigt og når jorden samtidigt (hvis underlaget er plant og vandret).

I praksis er det lidt vanskeligere. En moderne riffel skyder med projektiler og disse roterer på grund af riffelgangene. Luftmodstanden er modsat bevægelsens retning men den følger ved store hastigheder en andre gnidningslove. Desuden kan projektilet blive påvirket af aerodynamiske effekter.

Radarmålinger på en riffel med udgangshastighed 830 m/s viser at på 300 m er projektilet faldet 0,715 m og der er gået 0,3918 sek. Dette resultat er målt med radar. Her er tale om et langt projektil på 0,338" eller 8,6 mm i diameter og vejer 19,44 gram (altså større end mange riffelprojektiler) til finskydningsbrug. Et tilsvarende projektil som frigøres i samme højde kan man beregne faldtiden for med følgende formel(luftmodstanden betyder ikke noget ved disse små hastigheder):

t² = s/(½g)

Indsætter man s = 0,715 m og g = 9,815 m/s² (København) får man for tiden, t = 0,382 sek., for Nuuk hvor  g = 9,823 m/s² fås t = 0,3815 sek. I begge tilfælde falder den ikke afskudte kugle hurtigst.

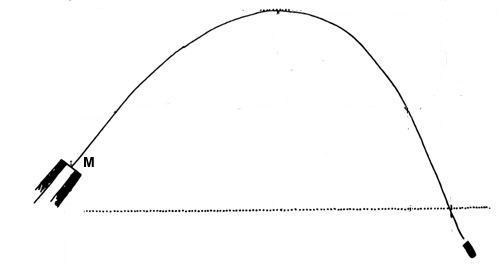
  Kasteparabel

Med venlig hilsen
Malte Olsen