Henfaldstider for radioaktive stoffer
Hej Spørg om Fysik
Tænkte om I kunne forklare om henfaldstiden på radioaktive stoffer? Har kigget på forskellige sider men det er stof der er lidt svært at forstå. Så tænkte om vi kunne forklare det bedre. Jeg ønsker en let forklaring på, hvad det er, men mest hvordan henfaldstiden kan regnes ud.
Niveauet må meget gerne være gymnasial.
Med venlig hilsen
M F
Antoine Henri Becquerel Nobel pris 1903 (F, 1852 - 1908) opdagede den naturlige radioaktivitet i 1896. Han ville undersøge Røntgenstråling (opdaget 1895) ved at lægge et fosforescerende stof på fotografiske plader. Han valgte et uransalt som fosforescerende stof.

Antoine Henri Becquerel
Da forsøgene skulle foregå i lys, forberedte han forsøget ved at pakke uransaltet og fotografisk plade ind i sort papir, det foregik naturligvis i mørke. Han opdagede, at pladerne allerede var eksponeret også uden røntgen og gengav formen på uransaltet, der var lagt på (se billedet hvor han har lagt et metalkors imellem). Han undersøgte derefter denne spontane proces, kernestråling. Senere opdagede man mange andre tunge stoffer gav samme typer af stråling bl.a. thorium. Især blandt de atomkerner med stor kernemasse findes en række ustabile stoffer f.eks. Uran, Radium og mange flere. Også visse lette stoffer er radioaktive på samme måde.
Stofferne viser sig ved henfald at udsende det, man kalder ioniserende stråling (det ioniserer luften) α -, β -, og ϒ - stråling. Når de henfalder omdannes de derved til andre grundstoffer, hvis det er α -, β - stråling. Se også: https://www.nbi.ku.dk/spoerg_om_fysik/fysik/radioaktivitet/ .

Foto af Becquerel, bemærk skyggen af metalkorset
Ved nærmere undersøgelse viser radioaktive henfald sig at være en statistisk proces, dvs. en given kerne har en bestemt chance for at henfalde i løbet af en given tid. Forskellene på forskellige stoffer viser sig at være, hvor mange kerner af et givet antal, der henfalder pr. tidsenhed, ud over forskelle i den energi som Heliumkernen (α - stråling) og elektronen (β -stråling) samt den elektromagnetiske stråling (ϒ - stråling) der kommer i processen har. Grunden til ustabiliteten kan være, at der er et meget ulige forhold imellem neutroner og protoner i kernen, at der er overskud af kernepartikler eller at kernen har overskud af energi. Da det er et rent statistisk fænomen, det man kalder en stokastisk proces, dvs. man kan kun beskrive en bestemt kernes chance for henfald indenfor en given tid med en sandsynlighed. Den ene kerne påvirkes ikke af at andre henfalder, derfor viser strålingen fra et radioaktivt stof sig at være en aftagende ekspotentialfunktion. Man kan indføre en henfaldskonstant, k, som er henfaldssandsynligheden pr. tidsenhed. Har man til start et givet antal kerner N0 og vil beskrive, hvor mange kerner man har N(t) til tiden t, kan det i et sådant tilfælde skrives, som det lille antal der henfalder ΔN(t) i en given kort tid Δt, og det kan skrives
ΔN(t) = - k N(t) * Δt
Der står at antal henfaldne kerner er proportionalt med tiden og antal kerner ved start. Heraf fås matematisk
N(t) = N0 * e -k*t
Hvis T½ kaldes halveringstiden, og det er den tid der går inden halvdelen af den oprindelige mængde radioaktivt stof er henfaldet, får man ved indsættelse af N(t) = N0/2 og t = T½
N(t) = N0/2 = N0 * e -k* T½ kan også skrives N/(t) = N0 * (½) t/T½
På grafen ses det at hver gang man halvere mængden af kerner på y-aksen går der samme tidsrum vist på x-aksen. Fra udtrykket herover ved at indsætte t = T½ svarende til N(t) = N0/2
T½ = ln2/k
Det man i praksis måler er ikke hvor mange kerner af de oprindelige, der er tilbage, det er det man kalder aktiviteten, A(t) som er antal henfald pr. tidsenhed ,
A(t)= ΔN(t)/Δ t= N0*k* e -k*t= A0 * e -k*t
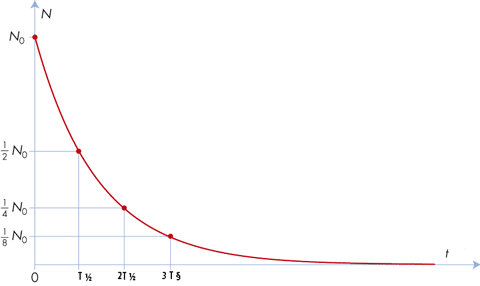
Henfaldskurve med halveringstider
Heraf kan man så principielt beregne k og T½ efter en måling af strålingen fra et radioaktivt stof, som funktion af tiden. Man måler så en del af den viste kurve og finder halveringstiden (det kan gøres for en ret lille del). Der er også sammenhænge imellem energierne strålingen udsendes med og halveringstiden. Endvidere kan man f.eks. i uranlejer måle forholdet imellem de forskellige isotoper, og finde ud af hvor lang tid det ville tage at nå dette forhold afhængigt af halveringstiderne, hvoraf man kender de korte godt.
Halveringstiden varierer indenfor meget vide grænser, og hver isotop har sin egen halveringstid. Som eksempel thorium 23290Th atommasse 232 og med 90 protoner i kernen har en T½ =. 1,41*1010 år (længere end solsystemet har eksisteret), 21890Th har T½ = 0,11 μs, og det er hverken de længste eller korteste kendte. Et af de stoffer som bør interesserer os alle er Kalium 4019K, 0,012 % af det naturlige kalium der er i maden, er denne isotop (og vi kan ikke leve uden kalium vi har normalt 100 - 150 mmol/l legemsvæske). Den har T½ = 1,26*109 år og bestråler os altså inde i kroppen i ganske ringe grad.
Ved f.eks. uheld på atomkraftværker kan der komme en iodisotop 13153I ud i atmosfæren.
Halveringstiden er T½ = 8,02 døgn. Den er farlig fordi al iod, vi får ind i organismen, samles i skjoldbrudskirtlerne foran på halsen og bestråler disse. Historisk beskytter man personer ved på forhånd at fylde depoterne med iod i tabletform, så det radioaktive udskilles.
Radioaktive isotoper bruges på hospitalerne til en række undersøgelser. Det er normalt isotoper med kort henfaldstid som hurtigt forsvinder så organismen ikke udsættes for vedvarende stråling. Til kræftbehandling bruges stråling f.eks. røntgenstråling men også radioaktive stoffer som cobolt 6027Co bruges til bestråling. En række meget kraftige radioaktive præparater bruges til at gøre engangssprøjter, injektions nåle og i tilfælde hvor det er tilladt visse fødevare (f.eks. krydderier) bakteriefrie. Det kan også gøres med røntgen. En vigtig anvendelse af radioaktive stoffer er tracer metoder, hvor man mærker et bestemt organisk stof med en lille smule af en radioaktiv isotop, dvs. man indbygger isotopen i stedet for et normalt ikke radioaktivt tilsvarende atom. Man kan så i planter og dyr følge, hvor den pågældende kerne bliver af, i de biologiske processer der sker i de pågældende organismer. Endeligt kan kraftige radioaktive præparater anvendes til kontrol af svejsninger, samlinger mm.
Radioaktive stoffer findes overalt i naturen se f.eks. https://www.nbi.ku.dk/spoerg_om_fysik/fysik/halveringstid_uran238/, men normalt i mængder som vi ikke kan konstatere skader os i det daglige.
Et af de radioaktive stoffer der opstår i de radioaktive henfaldskæder (efterkommere af 23290Th, 23892U, 23592U som findes i naturen, og den menneskeskabte 24194Pu) af de tunge stoffer se https://www.nbi.ku.dk/spoerg_om_fysik/fysik/radioaktivitet/ er Rn (Radon) som er en luftart. Den siver op af jorden og kan påvirke vores helbred hvis kældre, krybekældre mm., ikke er tætte og ventillerede.
Med venlig hilsen
Malte Olsen
