Hvordan måler man det absolutte nulpunkt.....og afstanden til stjernerne?
Hej Spørg om Fysik
Jeg er af mine kursister blevet spurgt om, hvordan man måler de ekstremt lave temperaturer, som blandt andet findes i rummet. -273 grader, som er det absolutte nulpunkt, hvordan måler man det?
Hvordan måler man afstanden til en stjerne? Lysår er en måleenhed, som jeg kender, men hvordan ved man at lyset har været så lang tid undervejs?
Med venlig hilsen
J N
Temperaturen er et mål for den energi et legeme har. Det absolutte nulpunkt, dvs. den lavest mulige temperatur, kan findes til -273,15 °C.
Planckkurver
Tilføres energi stiger temperaturen (primitive ildbor, skivebremser, bevægelsesenergi tilføres), fjernes energi afkøles emnet f.eks. tag lidt sprit på hånden, pust hen over så det fordamper, og man føler afkølingen, fordi fordampningen kræver energi.
Man kan også i princippet måle temperaturen af en luftmasse ved at finde molekylernes middelhastighed. Det kan vises, at sammenhængen er: c2 = 3RT/(N0*m), hvor c er molekylernes middelhastighed, R er gaskonstanten, N0 Avogadros tal, m er molekylmassen og T den absolutte temperatur.
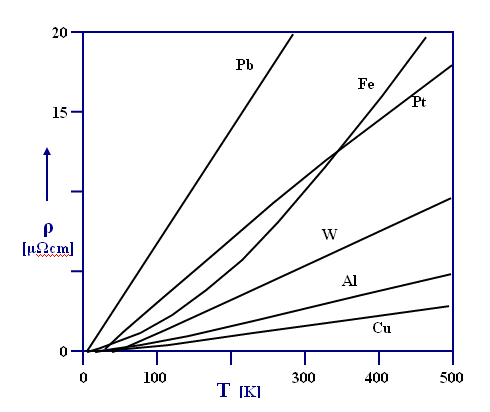
Modstandskurver ned til nært det absolutte nulpunkt for metaller, platin er meget brugbar
I atmosfærisk luft ved normale omstændigheder bliver hastigheden ca. 500 m/s i brint tilsvarende 2000 m/s. Man kan således omvendt måle temperaturen, hvis middelhastigheden kendes, også selv om der kun er meget få molekyler pr cm3. Man kan bl.a. få meget lave temperaturer i en gasmasse ved med passende LASER udstyr at bremse atomer eller molekyler ned til lavere middelhastigheder. Laserkøling >>
Måling af lave temperaturer
Den klassiske metode er termometre, som vi kender dem. Med passende væske kan man lave termometre til ca. -200 grader. Er vi her på jorden, er der en række muligheder.
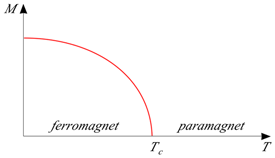
Cupieloven som viser magnetiske egenskaber i visse stoffer kan bruges til temperaturmåling
Den elektriske modstand i de fleste metaller aftager pænt jævnt imod en slutværdi nær det absolutte nulpunkt, f.eks. ses på grafen at en række metaller, at være lineært voksende/aftagende, og det kan forlænges til i nærheden af det absolutte nulpunkt, man kan så måle på de metaller. Der findes også en række velegnede halvledere.
Væsker
Helium er en væske ved 4 K (4 grader fra det absolutte nulpunkt), man kan måle trykket over væsken og trykket vil aftage lineært, når man køler, til lidt lavere temperaturer kan anvendes en anden heliumisotop, der hedder helium 3(normalt Helium er to protoner og 2 neutroner, Helium-3 har kun 1 neutron). Man opnår bl.a. lave temperaturer ved at fordampe væsker, f.eks. brint eller Helium-4 som normalt koger ved ca. 4 grader, men pumper man gassen væk så trykket bliver lavere, så falder temperaturen, man kan komme ned omkring 1 K og med He-3 lavere, og ved på en snedig måde at lade helium 3- fordampe ind i Helium – 4 kan man nå ca. 0,01 K.
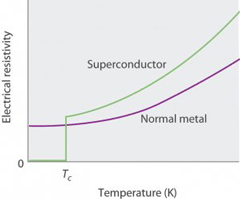
Superleder, den grønne kurve viser at modstanden i superlederen bliver 0 ohm ved en betemt temperatur
Magnetiske egenskaber
En række stoffer har magnetiske egenskaber, som man kender ændringen af, nært det absolutte nulpunkt, noget der hedder en Curie-lov, den kan bruges til at se temperatur ændringer ved lave temperaturer.
Superledning: En række metaller bliver superledende ved helt bestemte temperaturer. Det kan mål ved at komme dem i en lille spole med vekselstrøm, og så måle impedansen (vekselstrømsmodstanden), man kan så se, når de bliver superledende og kender så temperaturen.

Kryostat det er en "termoflaske" til flydende Helium hvor man laver eksperimenter ved lav temperatur
Hvis en gas opvarmes vil den før eller senere lyse (gløde). Atomernes elektroner kommer op i højere energiniveauer. Ved at se på atomers energiniveauer, kan man altså også måle en temperatur
Anbringer man elektroner eller atomkerner i et kraftigt magnetfelt og sætter man så samtidigt et vekselfelt på kan man lave noget der hedder elektronspin henholdsvis kernespin resonans, kernerne flipper op og ned (kernespinresonans anvendes på hospitaler til patientundersøgelser). Den nødvendige frekvens der skal til for at dette sker, afhænger af temperaturen på kendt måde, så det kan bruges til at måle temperaturen med. Man kan med magnetisk køling få elektronerne ned på ca. 10-9 K, man kan også med kraftige superledende magneter få atomerne med ned.

Indmad til en kryostat her noget man kalder en blandingskryostat hvor helium-3 fordamper ind i helium-4 og man kan nå omkring 0,001 K
Strålingstemperatur
Vi ved alle at en varm ovn eller et bål stråler så man kan mærke strålevarmen. Det gælder også til lavere temperaturer. Strålingen følger en lov som kaldes Plancks strålingslov (efter Max Karl Ernst Ludwig Planck (D, 1858 – 1947). Den står der noget om i Bestråling af hud med infrarød stråling >> og Temperaturstråling >> det kan også bruges til temperaturmåling ved lave temperaturer, selv om det er ret vanskeligt
Den laveste dokumenterede temperatur jeg har fundet opnået i et stykke metal, Rhodium, er 100 pK (0,1 milliartedel Kelvin), Finnerne er eksperter.
Næsten alle informationer vi har om rummet kommer fra elektromagnetisk stråling dvs. i ikke ringe grad lys, men også radiobølger og ioniserende stråling som røntgen. Det gælder afstande, bevægelser og temperatur, Temperaturen i rummet kan i mange tilfælde findes som stråling se: hvor skete bigbang >> Man kan også få oplysninger fra spektres intensiteter fra atomer i rummet, altså temperaturen findes fra det lys, de radiobølger osv. man kan observere. Farven f.eks. blålig betyder meget høj temperatur, rødlig lavere.
Afstande i universet
Når jorden bevæger sig rundt om solen vil stjerner i vores nærhed på fotografier af himlen flytte sig lidt i forhold til baggrunden. Ser man det, kan man ud fra den ellipse stjernen bevæger sig I, beregne afstanden se: Paralaksemetoden til astronomisk afstandsbedømmelse >>
En anden måde at måle afstande på er, at man ved observation af supernovaer, (stjerner der eksploderer - se: Hvor stor er en stjerne? >> ) afhængig af type, har nogen bestemte lyskurver for deres udstråling.
Man kan så måle udstrålingskurven for supernovaer i fjerne galakser, og derfra beregne afstanden. Supernovaer, hvor gasskyen fra eksplosionen kan ses, giver specielle muligheder. Krabbetågen, som er vist på fotoet, eksploderede i 1054 i stjernebilledet Tyren, gasskyen ses at bevæge sig imod os med en hastighed på ca. 1500 km/s målt med dopplereffekten, og ud fra den målte vinkelforøgelse af gasskyens størrelse, kan man beregne afstanden til ca. 6500 lysår, dvs. vi ved, hvor hurtigt kanterne flytter sig ud til siden, og hvilken ændring i den målte vinkel det giver, så kan vi beregne afstanden.

Paralaksemåling
Tilsvarende kan man bruge lyskurverne for andre variabelt lysende stjerner f.eks. cepheider se Hvorfor pulserer Cepheider? >>.
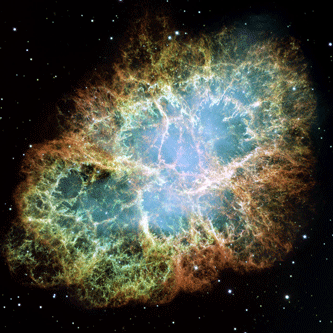
Krabbetågen
Endeligt kan man få oplysninger fra mere statistiske metoder f.eks. HR diagrammet, som er omtalt i en af henvisningerne ovenfor, ved at bestemme, hvor i diagrammet en given stjerne befinder sig ud fra dens spektre, og den lysstyrke, man ser.
Lysåret er bare en passende længdeenhed, man bruger (et lysår er 9,461*1015 m), den anvendes ikke til selve målingen.
Med venlig hilsen
Malte Olsen
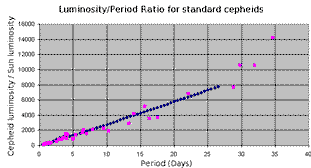
Cepheidernes lyskurver som funktion af perioden
